

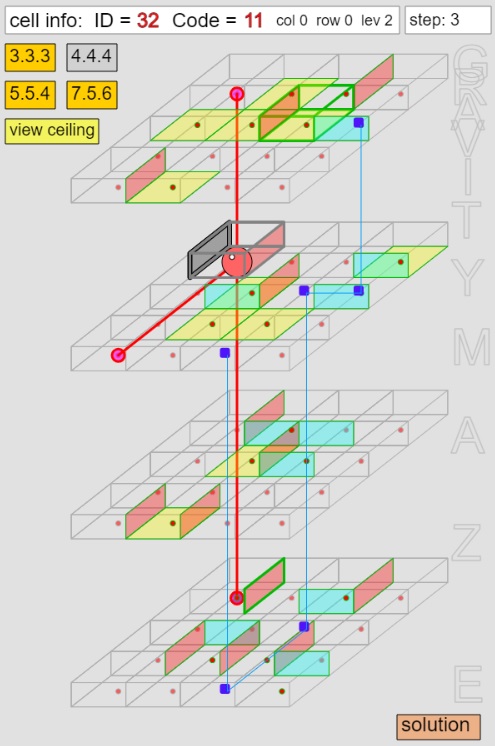
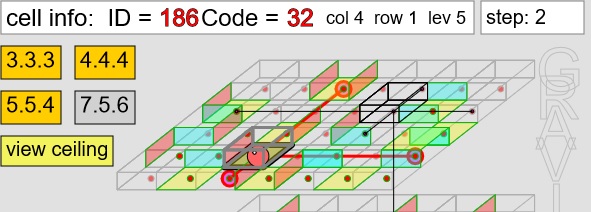
GRAVITY MAZE: a "strange" maze
The "strangeness" of this parallelepiped-shaped labyrinth is certainly not that of simulating the three dimensions, but of simulating the overturning of its base, so that the ball that runs through it "falls by gravity".
This movement mechanism creates paths from which one cannot go back and in any case not all directions are allowed, but only those determined by the conformation of the "cells" of the labyrinth and by the direction of entry into them.
The program is not complete but it works, and
I apologize but I haven't translated all the names and comments yet.
The examples for now are perhaps too simple: if you read the instruction at the end of code, you can do them yourself.
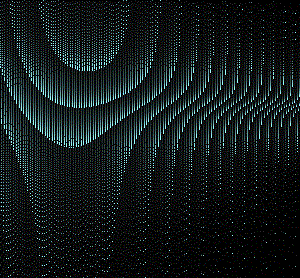
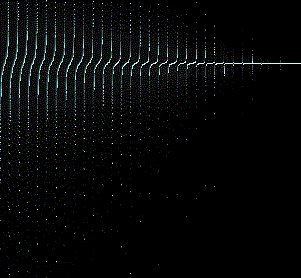
CASCADE OF POINTS: trigonometric "lace"
I wrote this program before knowing Processing or other languages dedicated to creativity. I liked the idea of creating beautiful trigonometric graphs but "far" from the periodic trend which usually features renderings based on the sine and cosine functions. So I first used a function containing third degree terms, trigonometric functions and parameters. As the values change, I DID NOT draw the graph joining the subsequent points with segments BUT I have drawn simply the points; in fact, the course of the lines would have been very confusing because at each cycle the values of Y "jump" up and down continuously. Instead the points drawn cycle after cycle are ordered and create suggestive patterns.



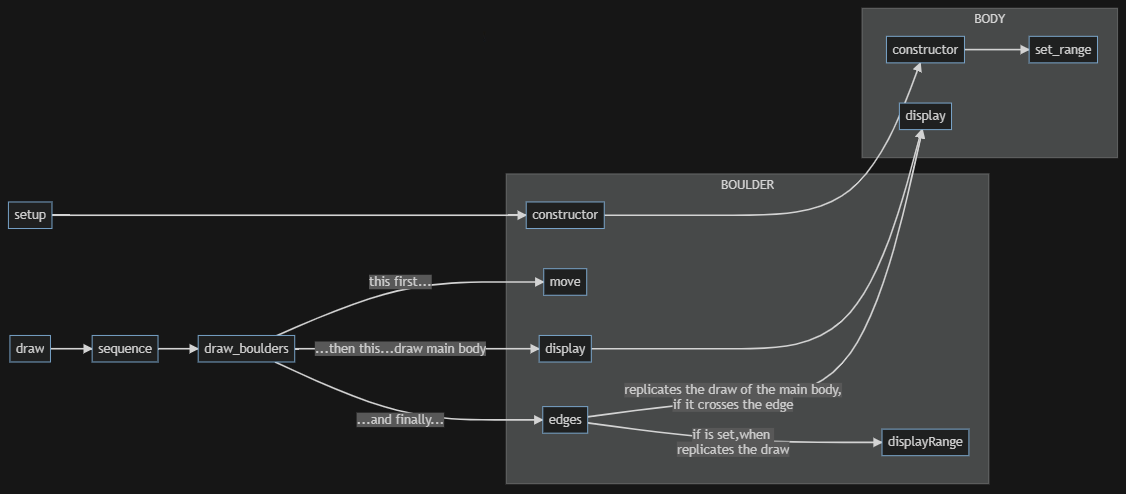
Modular: Rotations in a modular space
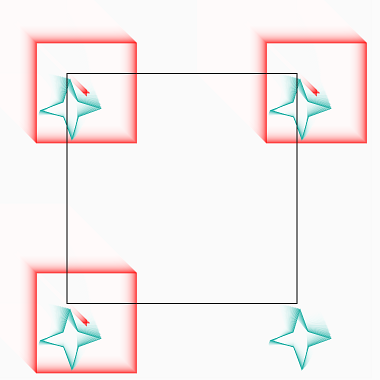
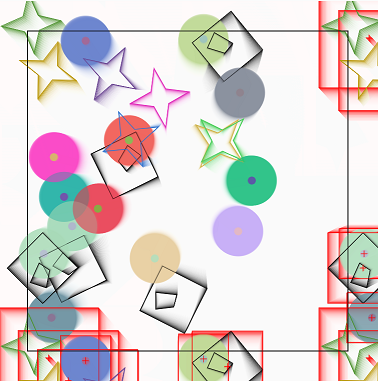
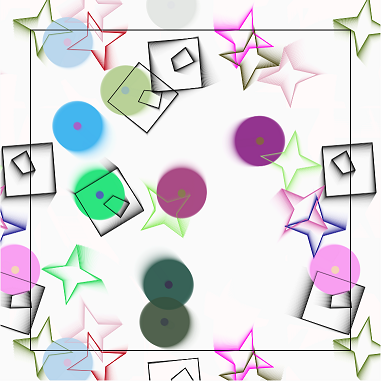
This program produces a drawing in which the objects, when they cross over
the edge, are also drawn on the opposite side.
If they cross a corner of the edge, they must be drawn four times.
If they cross one side of the edge, they must be drawn twice.
This "modular" way of drawing objects is the one used for static drawings in the "regular tessellations" of the floors or for the animations of famous games such as "Asteroid".
In the event that the objects rotate, the maximum encumbrance of the rotation must be considered, otherwise the position of each vertex of the object would have to be calculated each time.